omputers are dumb. They can do amazing things, but they are dumb. They are pretty needy too. We give them what they need and what they need is electricity. This is where the ones and zeros come in.

A one is the presence of electricity. A zero is the absence of electricity. Think on and off. Same thing. Electricity’s presence (one) and absence (zero) make a computer tick.

In fact, you have just learned the most basic code of computers. That was quick. One is presence and zero is absence. One is on and zero is off. This particular code is called binary. Now when you hear coders talk about binary, you know what they are referring to. Ones and zeros. That is it. Those ones and zeros are not that magical now huh?

Most coders don’t really care about the presence or absence of electricity though. Myself included. Coders just care that binary represents one of two states. State 1 or state 0. State on or state off. State true or state false. Ultimately the two states can represent anything you want. State color or state grayscale for example. Only one is active at a time. You get the idea.

For binary code, the computer takes the presence or absence of electricity in (input) and we convert meaning out (output). What makes binary code a code is that it is a system for converting meaning between forms. Etch this in your brain.

Code is a system for converting meaning between forms.

I could take a pencil and write a 1 or a 0 on a sheet of paper (or any two distinct symbols for that matter). I could then give it to you. As long as both of us agree on the converted meaning, then we would have a binary code to communicate. For example a 1 could mean "yes" and a 0 “no”. We could ask each other questions verbally and respond in this code.

There is nothing inherently magical about code. Remember this fact.

Computers take electricity as input. People convert meaning as output. Specifically, people have agreed that the presence of electricity is 1 and the absence is 0. Go take a look at the power buttons of various devices around you.

I will wait.

You will see that most, if not all, have a graphic combining a line symbol (1) and a circle symbol (0). Binary switch. On and Off. Cool.

How do we actually control electricity though? We can’t reliably use binary code to convert meaning in a computer if we cannot control electricity now can we.

Welcome to the electric circuit. It has one job. Control the flow of electricity. How convenient. Presence and absence. On and off. One and zero. This is the exact point where we bridge the physical world (presence or absence of electricity in a circuit) and the virtual world (one or zero). Think hard to soft. Hardware to software.

We won’t go into the details of circuits because they exceed the scope of this book. If you are interested in learning more however, I highly recommend But How Do It Know? by J. Clark Scott. The designer in me wishes the book had a more communicative title in addition to a more timeless cover design, but I digress. J. Clark Scott does an amazing job teaching how computers and their various components work. As important, he teaches in a very easy-to-understand and digestible fashion. Get the book if you want to learn how computers work. Soapbox dismounted.

Scott’s book is not required reading to move forward though. Just know that the amount of binary states that can be represented physically (electrically) and thus virtually (code) in a computer, is more than you need. Additionally, computers are fast because electricity is fast. For example electricity can revolve around Earth's equater roughly seven times in one second. Think about that again. Your creativity and experience are the only limiting factors.

Bridging the physical to virtual gap is the fundamental aspect that enables computers and the amazing games, tools, and software we love, to exist.

A code with only two states is kind of boring. Useful yes, but boring. I bet you are thinking we can make a more interesting code if we have more than one binary. You are correct. Coders never say more than one binary though. It sounds weird. It also takes too long to say and type. Coders prefer shortcuts. Welcome to the word bit.

A bit is a binary digit. We already know binary represents one of two states. We also know that those two states are agreed to mean 1 and 0. So a bit is a binary digit. A bit can either be a 1 or a 0. Simple.

One bit is boring because it can only represent one of two states. The natural question is then, how many states can we represent with two bits?

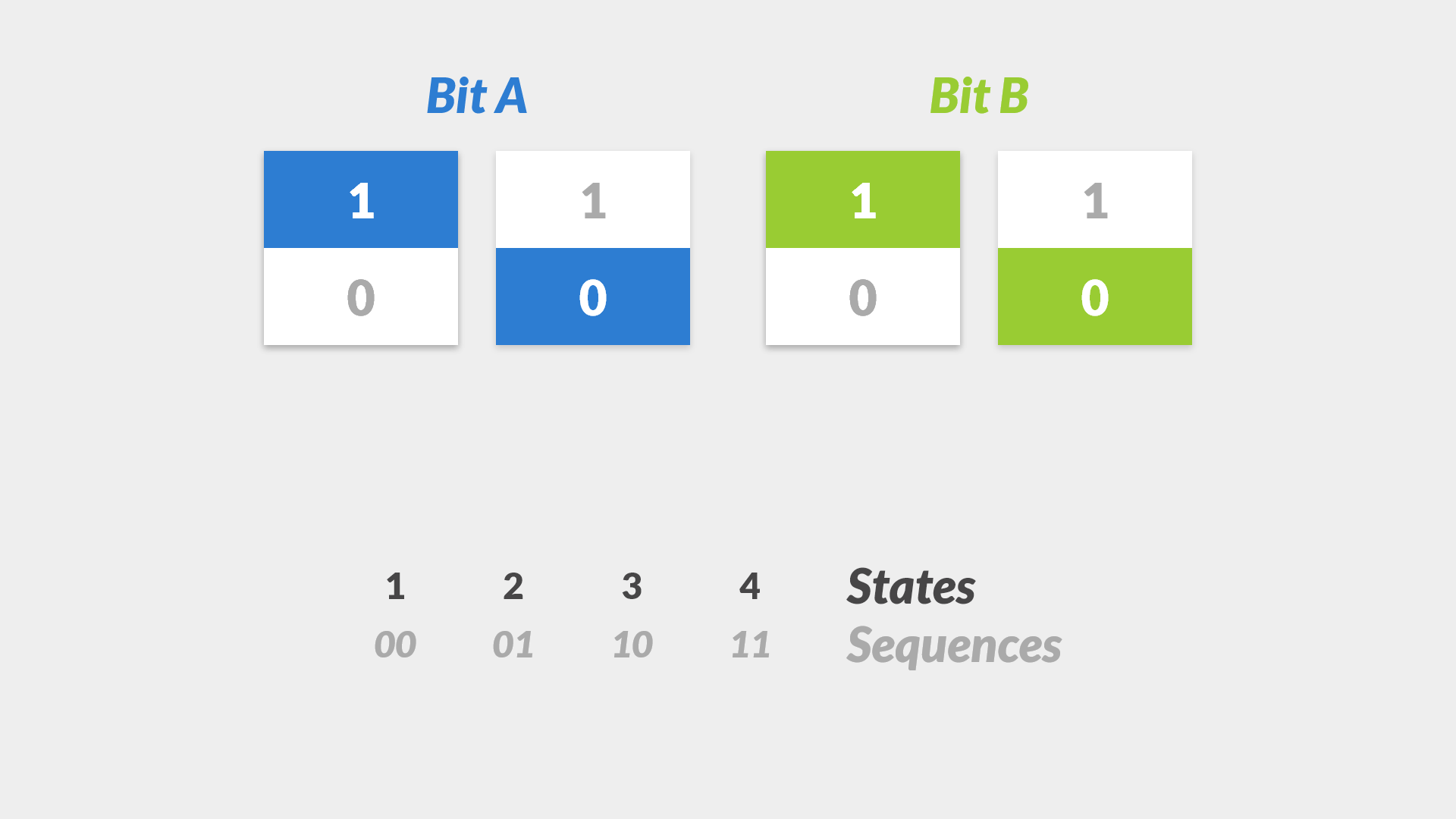
That makes sense. One bit represents one of two possible states. Two bits represents one of four possible states. No brainer.

Those 00 or 01 or 10 or 11 sequences look weird though right? They are. Thankfully, when we get to writing our own code, we don’t have to write in 1s and 0s. As a designer, I would not have learned to code otherwise.

Now is a good point in time to reflect on why we are even looking at bits if we don’t have to code with them. There are four ideas worth instilling:

1. Computers, these complex machines, rely solely on extremely basic concepts
2. There is no magic in coding, just simple ideas stacked atop each other
3. The one-of-two-states concept a single bit represents is constantly reused in coding
4. The longer the sequence of bits, the greater the amount of states

How many states could we represent with three bits?

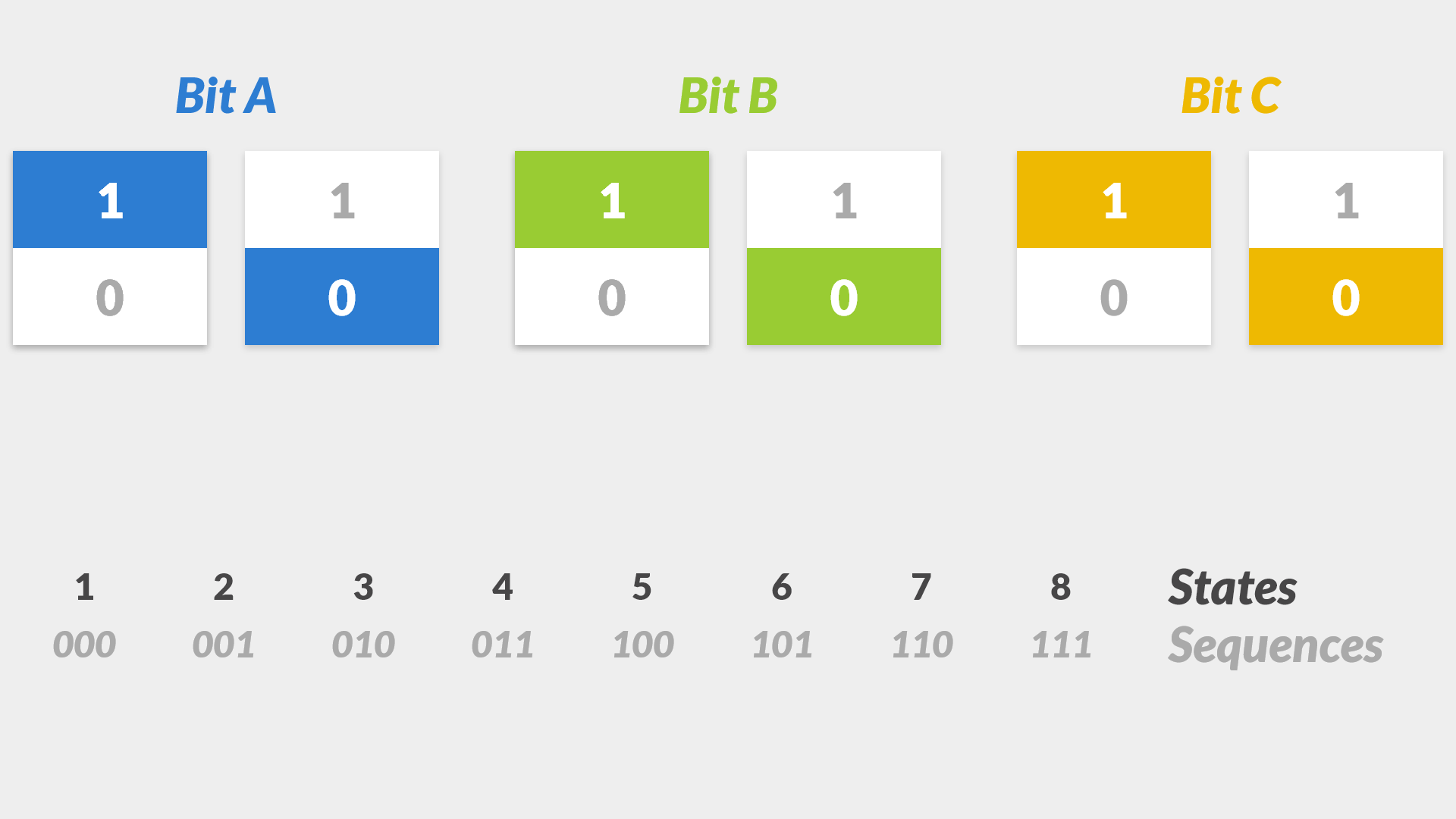
Eight? I was expecting six. It makes sense though when we see each state's bit sequence. For every bit we add, we double the total possible number of states as before.

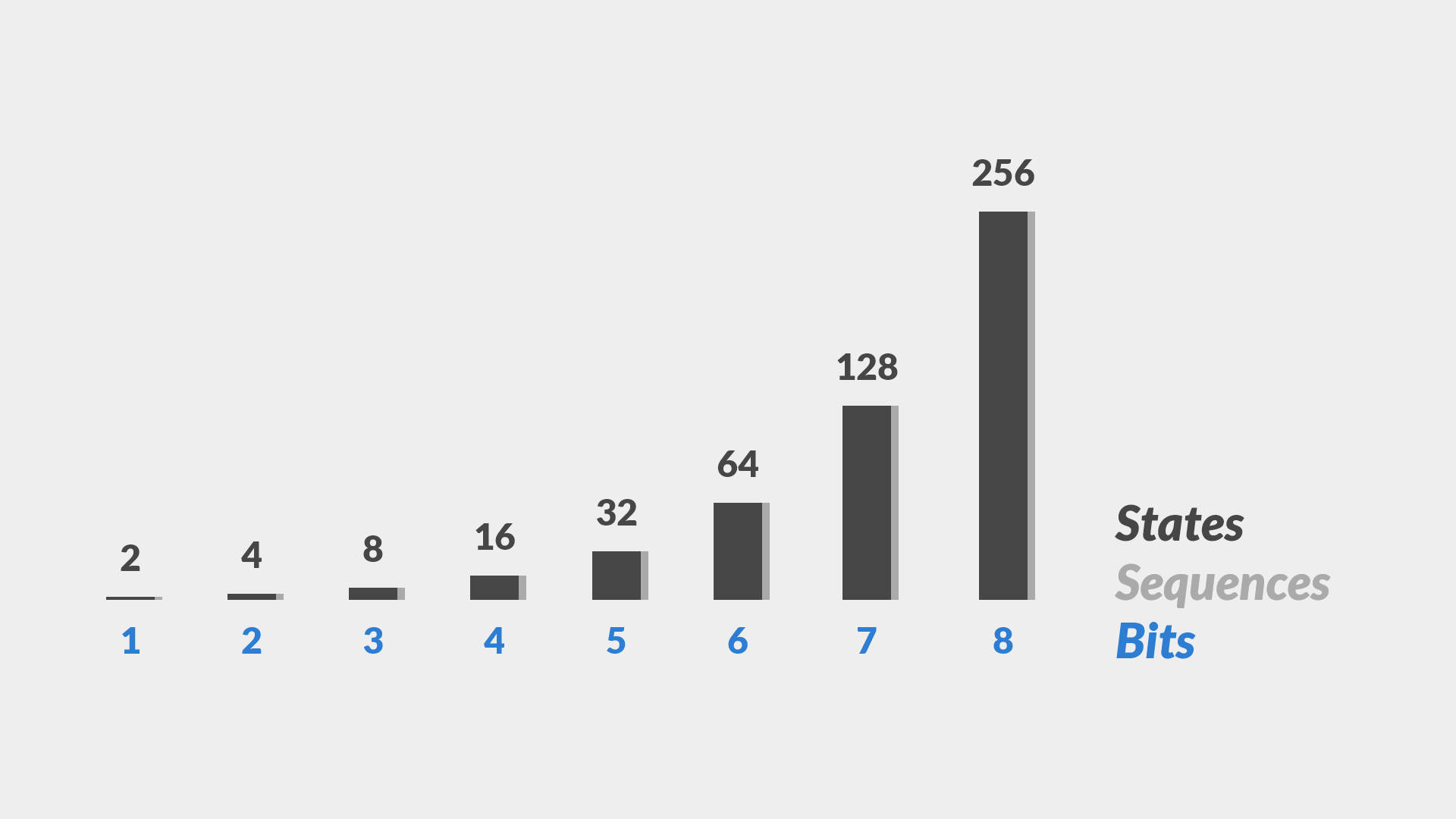
You will notice that I stop at eight bits in the example above. We could keep going and the same doubling rule would apply. Why stop at eight then? Random I know. Ultimately, people simply agreed that eight is a good stopping point. They agreed that being able to represent 256 states was good enough for a wide range of codes. Again, no inherent magic.

We know coders like shortcuts. Is there a shorter way to say and type eight bits? Yes, welcome to the word byte. A byte is eight bits. Naturally, a byte also represents one of 256 states.

Let’s use what we just learned to make an example code of our own. We will use a byte’s 256 states to represent the symbols of the English language. Twenty-six lowercase and twenty-six uppercase letters would use up fifty-two states. Ten numerals and all the punctuation marks, including a lot of obscure marks, could be represented in another fifty states. We could increase fifty to one-hundred and include even more obscure marks (poop emoji included). One hundred four unused states would still remain (256 - 26 - 26 - 100 = 104). Good enough, for English at least.

What if we wanted a code to represent all the symbols of every single human language we have ever known? A single byte would not cut it. Different amounts of bits, and thus bytes, are useful for different scenarios. Chew on that.

I want to reinforce the notion that the converted meaning represented by a certain number of states could be anything we want. This is why coding is such an expressive and creative craft. This foundation of binary, bit, and byte is simply about representing states. As the amount of states a computer controls increases, so too does the potential power of the code we author.

I mentioned previously that we don’t have to write code in 1s and 0s. Thank god. Coders have done that for us already. Then other coders created their own code on top of that. This stacking of code on top of code is what will allow us to write JavaScript later. We won’t care about any of the code underneath JavaScript. We will focus only on the high-level language of JavaScript. We will ignore the low-level languages beneath it. We will just know, and respect the fact, that they are there.

Get out your sketchbook and try to come up with your own binary code that represents a 2x2 black and white image. Seriously, try it. Feel free to use the visual output states below as a guide.

Your solution may differ from mine and that is fine. The goal here is simply to demonstrate how we can visualize a code. This is a primitive example with admittedly uninteresting output. Regardless, it provides one example of how to visualize a code.

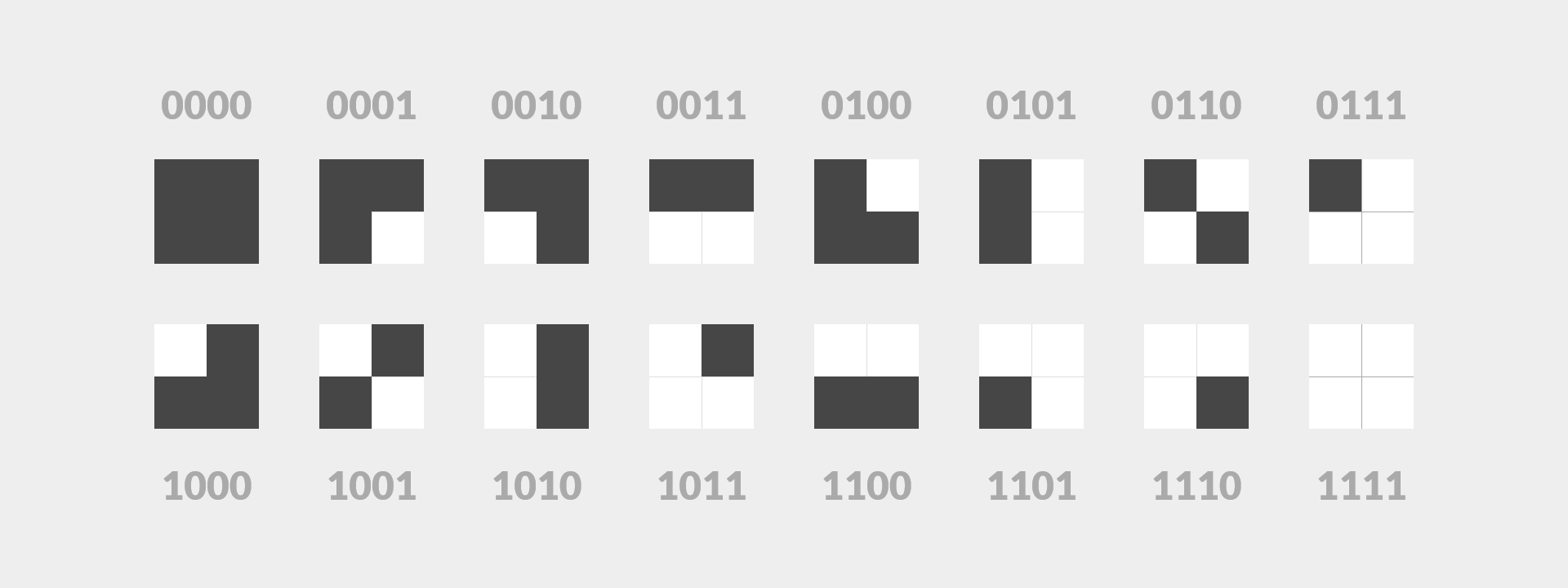
Each black and white square in the visual above illustrates a core aspect of computer graphics. If you author digital content you will have made the connection. Welcome to the pixel.

Pixel is another shortcut word. A pixel is a picture element. Do not ask me where the "x" came from. Simply put, to visualize a code on a computer screen, pixels are used. Naturally, the more pixels you have, the larger the image. Makes sense.

The sixteen variants above each represent a 2x2 four pixel image. They are represented in code using a 4-bit code (half a byte). If we used a full byte, then we could represent an eight pixel image that has two hundred fifty six variants. Technically speaking our image's dimensions, using the two hundred fifty six state variants, could be either:

• 1x8
• 2x4
• 4x2
• 8x1

Similarly, our 4-bit code could represent the image dimensions:

• 1x4
• 2x2
• 4x1

In either case, the underlying bits are simply a sequence of ones and zeros. The pixel count remains constant where the converted meaning of the bit sequence determines the image's dimensions. Generally speaking, the greater the pixel count, the more bits and thus bytes are required to represent it.

The above approach only allows for black and white images. As designers however, we greatly value the use of color to communicate within our creations. Take a moment before continuing and consider how might you code color?

Thus far we have made our own example codes. One to represent the symbols in the English language and another to represent black and white images. We could continue this trend. Instead we will transition toward codes that already exist. The advantage is twofold:

1. Less work for us, we don’t need to reinvent the wheel
2. Using established codes empowers us to achieve more, faster

In the context of color we will explore the common codes RGB and HEX. The former is red green blue and the latter is hexadecimal. We will start with RGB.

RGB is composed of three values (color channels). A red value, a green value, and a blue value. Combined they represent a specific color value. The literal color represented by a specific RGB coded value has already been decided. No work on our end. Nice. We simply rely on the various design applications we use to consistently represent colors in our digital designs. Figma, Sketch, Adobe XD, Photoshop, Illustrator, and Lightroom are a few examples of the hundreds, if not thousands, of authoring applications we depend on to consistently represent color.

RGB is represented in a few flavors too. Let's start with using a bit for each red, green, and blue value. We saw earlier in the Three Bits visual that we get eight states and sequences. Now we'll simply associate a color with each.

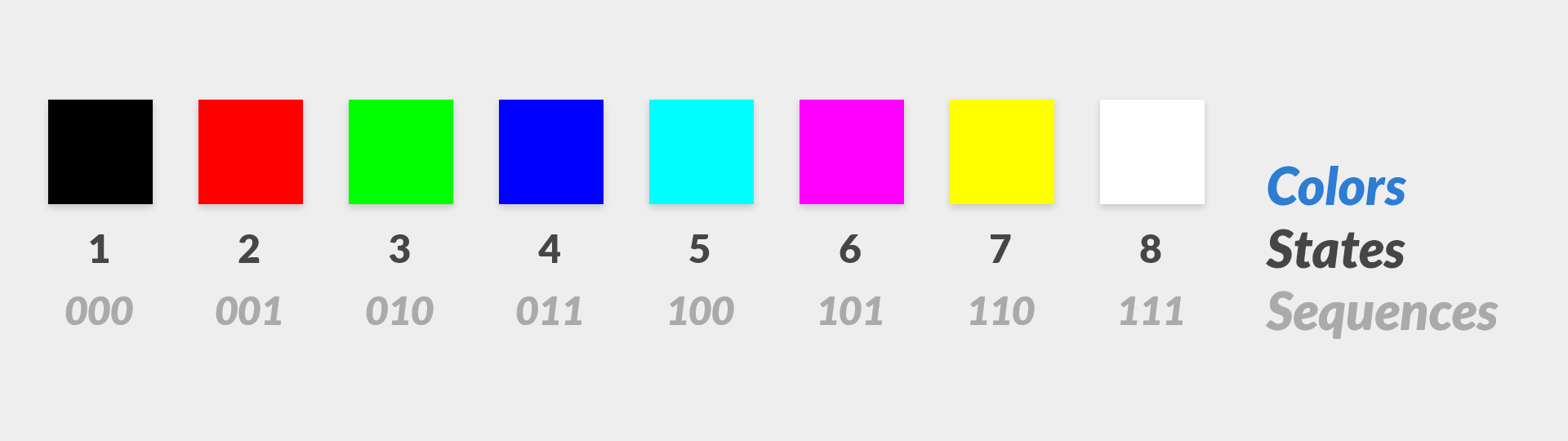
Eight colors is a pretty limiting palette. What happens if we swap out the bits for bytes?

Holy shit.

RGB gets us over 16 million color values. That palette is enormous. This is an actual flavor of RGB called RGB24. Another is called RGB32 or RGBA, where "A" is an alpha (transparency) value. Just call them by their normal names RGB and RGBA.

Here are the same eight colors seen above in the 3-Bit RGB visual, but with three bytes instead of bits.

You will notice the sample RGB colors above range from 0-255 for each byte’s value. If I invented the RGB code, 1-256 would be used instead. I did not invent it and instead we must use 0-255. Sad.

Counting starting at zero instead of one is a recurring pattern you will see in coding. This is one of the fundamental aspects that throws non-coders off when first learning more about coding. We have started counting from one not zero our entire lives. This is admittedly a difficult pill to swallow, but we must. Thankfully it will become second nature in time. Feel free to pursue clarity through zero-based numbering research however. For a quick and dirty answer, math nerds and computer optimization are to blame.

Hexadecimal is another common color code. It represents the same color range as RGB, just differently. Instead of a range between 0-255 for each R, G, and B value, HEX uses 00-FF for each. The letters A-F replace the numbers 10-15 (A instead of 10 through F instead of 15).

So for HEX, each color channel is represented by two characters (00-FF) instead of RGB's three (0-255). A minimalist designer can appreciate this. So too can an efficient coder.

Naturally, each character pair represents 256 values (16x16 = 256). Additionally, the # symbol often precedes the value. Example time with the same eight colors we've been using.

Feel free to continue to use color pickers, swatches, generated palettes, or any other tooling you use for color when designing. Moving forward you will simply be armed with a deeper understanding of how the color is coded. Or more precisely encoded.

Code is a system for converting meaning between forms. One form is considered encoded and the other decoded. To encode, is to convert into coded form. To decode is to convert from coded form. A few forms have been encoded and decoded already.

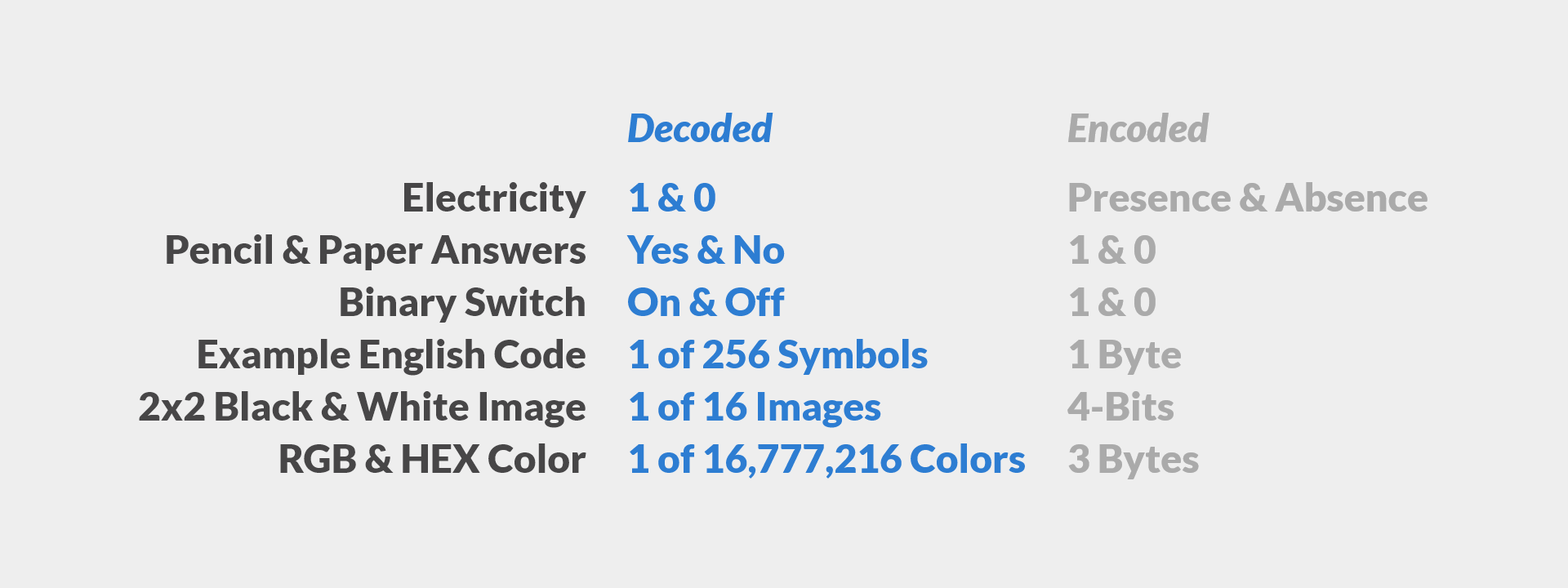
A decoded form can be another code’s encoded form. The opposite is also possible. Remember this. Different environments, systems, and software sometimes only work with a specific form. The internet, browsers, and design software for example, in addition to the operating systems they run on, all need to encode and decode to do the cool things they do. Having the capability to convert forms enables better communication with each other. Each software system may expand its own capabilities by having this conversion power too. Conversion through encoding and decoding is power.

Imagine a code where a bit’s two states encoded for two RGB colors. The bit’s 1 would represent white. The bit’s 0 would represent black.

What if we had to send this coded data over the internet from one side of the world to the other? Would you choose the encoded or decoded form?

Math is not my strong suit, but a single bit is twenty-four times smaller than twenty-four bits. In principle, the single bit will be delivered twenty-four times faster. Winning. This illustrates that the single bit is better for sending across the internet. However, once the bit arrives, it will not be understood as white or black until decoding occurs.

What if I told you that the decoding process took one hour? This is just a thought experiment, but if that was the case, then I would take my chances sending the twenty-four bits instead.

The takeaway here is that encoded and decoded forms are valuable in different scenarios. As illustrated above, the desire for fast internet often means encoding data before sending and then decoding upon arrival.

Let’s chain together everything we have covered thus far to save a color image.

Computers manage the presence and absence of electricity with circuits. These allow us to bridge the physical world (hardware) to the virtual (software). We agree that the presence of electricity is a 1 and the absence a 0. We refer to 1 and 0 as a binary code. Each 1 and 0 is a binary digit.

Saying and typing binary digit is annoying. Coders created the shortcut word bit to alleviate this annoyance. Naturally, a bit represents one of two states at any moment in time. Eight of these bits are a byte. A byte allows us to represent 256 states. The number eight is arbitrary. Representing 256 states was simply a good enough amount for coders. It was good enough because it could represent a wide range of codes. All the English characters and then some for example, can be represented within 256 states with ease.

Using three bytes (24 bits) allows us to represent over 16 million different states. Colors in our examples thus far. For the image to be saved we will simply encode bytes and save to a file. When a design application loads our image file, it will be responsible for decoding it. Since RGB and HEX are agreed upon ways to represent color, we can rely on the application to display what we intended. This only works if we let the application know how to decode it. Cool, that makes sense.

For simplicity we will create a one pixel image. Understanding how one color pixel is encoded means we can simply repeat the same process until we have as many pixels as we want. Again, coding uses simple, basic, repetitive, and reusable concepts. Not magic.

A single color will fit in our pixel. The color will be a random one of the over 16 million possibilities. How might you accomplish this? Try to sketch an approach before moving forward.

I simply flipped a coin eight times. Heads was 1 and tails was 0, my own little code. This resulted in a byte of encoded data. I repeated this process two more times. You know where I am going with this. Decoded, the three bytes represent one color. RGB or HEX will do.

Once encoded, we need to actually save it to a file. How do we do that? Well it is quite simple actually. The Operating System (OS) you run and use your design application(s) on (Windows, Mac, iOS, Android, etc.) has prewritten code giving you this power. Again, prewritten code stacked on prewritten code often gives us an easy way to accomplish tasks that would otherwise be more difficult and time consuming.

Long story short, the encoded data needs to be inserted into an empty file. When saving the file, it needs to have a file extension appended to the file’s name. Think .jpg, .png, .psd, .html, .css, and .js for example. The sole reason for a file extension is so the OS and its applications can quickly identify the file’s type. Why is that important? If you didn’t already guess, the file extension helps identify the decoding approach. In turn, only certain applications know how to work with certain file types.

Full circle.

Later, when we start to write our own JavaScript code, we will use the file extension .js. The code in the JavaScript file will not be in 1s and 0s though. Instead we will use the words that are part of the JavaScript language. We are not limited to just JavaScript words though, we get to use our own custom ones too. Much better than 1s and 0s.

First however, we will look at the three distinct concepts used to display static, dynamic, and interactive designs on a computer or device screen. These concepts are structure, style, and behavior. We will visit each in the context of 2D and 3D to better shape your perspective (pun intended). Go time.